Hypothesen testen

Wir wollen euch an dieser Stelle ein paar verschiedene Strategien für das Testen empirischer Hypothesen vorstellen. Zum einen die klassische Statistik und zum anderen Cohens Effektstärken und (wieder) moderne Bayssche Statistik.

Dabei starten wir mit fundamentalen Begriffen wie P-Wert, Signifikanzniveau, Fehler 1.- und Fehler 2. Art. Denn in sehr vielen wissenschaftlichen Projekten haben wir die Erfahrung gemacht, dass viele gar nicht genau wissen, was Signifikanz eigentlich bedeutet und wofür der P-Wert im Grunde steht. Die beliebtesten Ansätze sind dabei, dass Signifikanz mit „nicht zufällig“ „bedeutsam“ oder „wichtig“ erklärt wird. Das ist so nicht richtig, wenn auch die eigentliche Definition ist nicht besonders schwierig ist.

Was heißt „Signifikanz“?

Um Signifikanz zu verstehen, müssen wir uns anschauen, was es mit dem Fehler 1. Und 2. Art auf sich hat. Hier nehmen wir einmal das Beispiel eines Corona-Schnelltests. Aktuell (Stand: April, 2021) ein emotional sehr aufgeladenes Thema.

Wir gehen also einmal davon aus, dass du typische Krankheitssymptome (Fieber, Verlust von Geschmack, Husten etc.) hast und in die nächste Testambulanz gehst.

Fehler 1. Art & Fehler 2. Art

Ein Test kann immer fehleranfällig sein und aus der Kombination der möglichen Outcomes und Fehler ergibt sich folgendes Schaubild:

Ist ein Test in der Lage infizierte Personen als solche zu erkennen, spricht man von Sensitivität. Kann er nicht-Infizierte korrekt als negativ erkennen, von Spezifität.

Ein Test kann aber falsche Ergebnisse liefern. Falsch positiv heißt dabei, dass du keine Infektion mit SARS-Covid-19 hast, der Test dich aber als infiziert einstuft. Falsch negativ heißt, du bist infiziert, der Test übersieht dich aber. Das Ganze ist in der Praxis sehr relevant, denn:

Entscheidend sind also die Fehler des Tests. Bist du nicht infiziert, der Test wird aber falsch positiv, ist dies sehr ärgerlich und du musst umsonst 2 Wochen in Quarantäne. Entscheidender und viel relevanter ist aber der falsch negative Test. Du bist infiziert und infizierst deine Mitmenschen, musst aber fälschlicherweise nicht Quarantäne. Falsch positiv nennt man Alpha-Fehler (α), falsch negativ den Beta-Fehler (β).

Und hier kommt jetzt der P-Wert, auch bekannt als Signifikanzwert ins Spiel. Denn was wir hier mit Corona-Tests erklären, gilt vor allem für empirische Hypothesen und deren statistische Tests.

Wenn du postulierst, dass es beispielsweise einen Unterscheid zwischen zwei Gruppen hinsichtlich eines Merkmals gibt (T-Test), kannst du dich dabei natürlich irren. Es kann sein, dass du einen Gruppenunterschied annimmst, der aber nicht da ist (falsch positiv bzw. α-Fehler bzw. Fehler 1. Art). Hier müsste eigentlich deine Nullhypothese beibehalten werden. Das Gegenteil wäre der Fall, wenn du keinen Unterschied annimmst, jedoch einer besteht (falsch negativ bzw. β-Fehler bzw. Fehler 2. Art). Dies ist sehr ärgerlich, denn wir alle wollen ja signifikante Ergebnisse.

P-Wert

Was ist jetzt also der P-Wert. Der P-Wert ist die Wahrscheinlichkeit (Probability) einen α-Fehler zu begehen! Also von einem Effekt zu sprechen, obwohl eigentlich keiner da ist.

Eine etwas sperrigere Erklärung ist, dass der P-wert die Wahrscheinlichkeit ist, unter der Annahme, dass die Nullhypothese nicht verworfen werden kann, ein bestimmtes Stichprobenergebnis zu beobachten.

Beide laufen auf dasselbe hinaus. Ein kleiner P-Wert heißt also, eine geringe α -Fehlerwahrscheinlichkeit bzw. eine geringe Wahrscheinlichkeit einer Beobachtung unter der Annahme der Nullhypothese. Und daher hat beispielsweise das Signifikanzniveau-α seinen Namen.

Signifikanzniveau (auch Signifikanzniveau- α)

Hier haben sich in den letzten Jahrzehnten 3 Niveaus etabliert. 5% (vermutlich am häufigsten), 1% und 0.1%. Als Faktor also 0.05, 0.01 und 0.001.

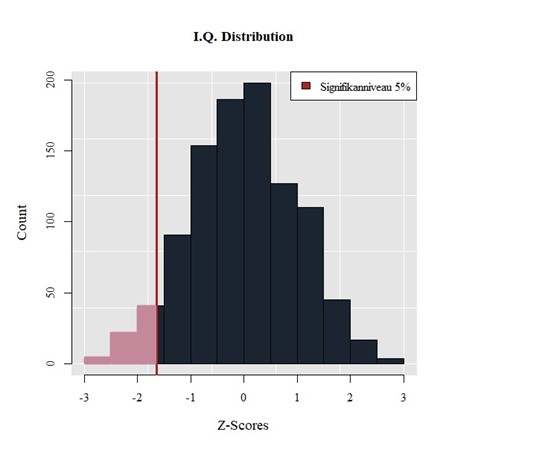
In der Abbildung ist eine zufällige Normalverteilung des IQ dargestellt. Ein Signifikanzniveau von 5% wurde gewählt und der einseitige Ablehnbereich (der Nullhypothese) markiert. Würde beispielsweise der Mittelwert einer zweiten Verteilung in diesen Bereich fallen, wäre der Unterschied signifikant.

Unterschreitet der P-Wert das Signifikanzniveau, spricht man also von Signifikanz. Und hier liegt nun aber die erste und eine der der größten Kritikpunkte am klassischen Testen. Woher kommen diese Signifikanzniveaus? Sie sind willkürlich gewählt und werden oft nach Belieben verschoben um am Ende doch noch signifikante Ergebnisse zu erhalten. Und wer sagt, dass ein 5% Alpha-Fehler nicht viel zu hoch ist?

Kritik am klassischen Testen

Die Kritik am klassischen Testen ist so alt wie diese Methode an sich. Zum Teil ist sie berechtigt, zum Teil aber auch nicht. Wir wollen euch die Kritikpunkte einmal erklären, damit ihr Studienergebnisse besser und kritischer Interpretieren könnt.

Alpha-Kumulierung

Neben der Willkür in der Festlegung des Signifikanzniveaus spielt die α-Kumulierung eine sehr große Rolle. Angenommen du hast nun Erkältungssymptome und willst dich auf SARS-Covid-19 testen lassen. Wir gehen davon aus, dass wir eine 5% α-Fehlerwahrscheinlichkeit bei Corona-Tests beobachten können. Was würde passieren, wenn du einfach 100 Tests machen würdest? Es würden wahrscheinlich 5 Tests falsch positiv werden! In 1 der 20 Fällen würdest du also angezeigt bekommen, dass du Corona hast, obwohl dies nicht der Fall ist. Das nennt sich Alpha-Kumulierung und entsteht durch multiples Testen. Je mehr Tests man macht, umso mehr Ergebnisse werden also zwangläufig signifikant, wenn man das Signifikanzniveau oder den P-Wert nicht korrigiert.

Tatsächlich stellt dies ein massives Problem in der modernen wissenschaftlichen Welt dar. Gerade im humanwissenschaftlichen Bereich werden in wissenschaftlichen Arbeiten dutzende oder zum Teil hunderte statistische Tests durchgeführt. Publiziert werden am Ende aber oft nur die signifikanten Ergebnisse. Diese sind dann wahrscheinlich nur α -Fehler. Und diese können dann letztlich nicht mehr repliziert werden.

Daher ist eine Anpassung der Signifikanzniveaus oder des P-Wertes erforderlich. Hier haben sich mittlerweile viel Verfahren etabliert, wie die Bonferroni-, Bonferroni-Holm-, Tukey T- oder Dunnet-Korrektur.

Einfluss der Stichprobengröße N auf den P-Wert

Ein weiteres Problem stellt der Einfluss der Stichprobengröße auf den P-Wert dar. In kleinen Stichproben brauchen wir schon starke Effekte, damit der Test signifikant wird. In sehr großen Stichproben hingegen werden minimale Effekte bereits hochsignifikant. Diese liegen zum Teil im Messfehlerbereich und werden dann dennoch publiziert.

Um den Einfluss der Stichprobengröße auf den P-Wert zu versanschaulichen nehmen wir an dieser Stelle die Formel des einfachen T-Tests für unabhängige Stichproben.

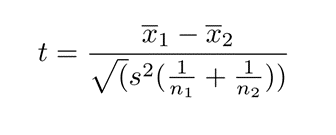
Hier wird das Folgende deutlich: Je größer die Stichproben (n1, n2) sind, umso kleiner wird der Term im Divisor und umso höher wird automatisch der Quotient, in diesem Fall t. Bei gleichen Mittelwertunterschieden zwischen zwei Gruppe, erhält man also in Abhängigkeit der Stichprobengröße unterschiedliche P-Werte. Wenn die Stichprobe groß genug wird, werden im klassischen Testen sogar Tests mit randomisierten Daten signifikant. Wir haben das einmal in einer kleinen Studie mit R und eigenen Zufallsdaten dargestellt:

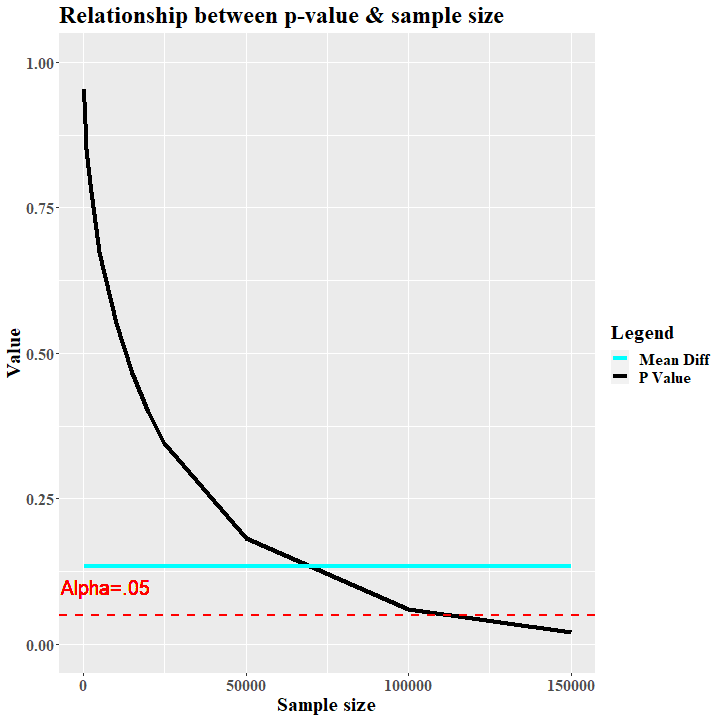
An dieser Stelle haben wir zwei normalverteilte Zufallsverteilungen gebildet. Im Randomisierungsprozess haben wir jeweils einen Mittelwert von 100 und eine Standardabweichung von 15 festgelegt. Damit bilden die beiden zufälligen Verteilungen nun den normalverteilten IQ ab. Die erste Zufallsverteilung soll dabei der IQ aus dem Jahr 2000 mit einem Mittelwert von 101.254 und einer Standardabweichung von 14.776 darstellen. Die zweite zufällige Verteilung ist der hypothetische IQ aus dem Jahr 2020 mit einem Mittelwert von 101.121 und einer Standardabweichung von 14.089. Der Mittelwertsunterschied in unserem Beispiel beträgt also lediglich 0.133 IQ-Punkte.

Es wird vermutlich den meisten einleuchten, dass IQ-Punkt bzw. ein Unterschied von Standardabweichung gar nicht messbar ist und eher im Bereich eines Messfehlers liegt.

Wenn wir nun diese zufälligen Verteiluingen mit den Größen N=100 mit einem T-Test für verbundene Stichproben testen, ergibt sich natürlich kein signifikanter Unterschied (t(99) = .059 , p = .952) Unser P-Wert ist weit entfernt von 0.05 (s. Abb. 2).

Wenn wir aber im nächsten Schritt die Stichprobe um den Faktor 10 vergrößern, sieht es anders aus. Die Daten bleiben dieselben. Der Mittelwertsunterschied zwischen beiden Verteilung bleibt gleich (s. Abb.2, Mean Diff). Deskriptiv ändert sich nichts außer der Stichprobengröße. Was sich aber ändert ist der P-wert. Im T-Test ist dieser nun leicht gefallen (t(999) = . 188, p = . 850).

Bei einem N von 110000 unterschreitet er dann sogar das Signifikanzniveau, obwohl es sich um gleich randomisierte Zufallsdaten handelt (t(109999) = 1.978, p = . 047; s. Abb. 2). Natürlich kann man jetzt argumentieren, dass eine sehr große Stichprobe eher robuste Ergebnisse liefert und der Effekt eher repräsentativ ist. Es ist zudem wahrscheinlicher, dass ein Effekt tatsächlich vorhanden ist. Problematisch wird diese Argumentation aber eben, wenn winzige Effekte, die auf Mess- oder Rundungsfehlern basieren, signifikant werden. In unserem Beispiel haben wir also einen signifikanten Unterschied zwischen zwei gleich randomisierten Verteilungen gefunden und würden mit hoher Wahrscheinlichkeit einen α-Fehler publizieren. Doch so etwas muss nicht passieren.

Alternativen zum P-Wert - Der Bayes Faktor und die Effektstärke

An dieser Stelle wollen wir euch zwei Alternativen zum klassischen Testen vorstellen, die das Problem der α-Kumulierung und der Abhängigkeit von der Stichprobengröße zum Teil umgehen können.

Einfluss der Stichprobengröße N auf die Effektstärke

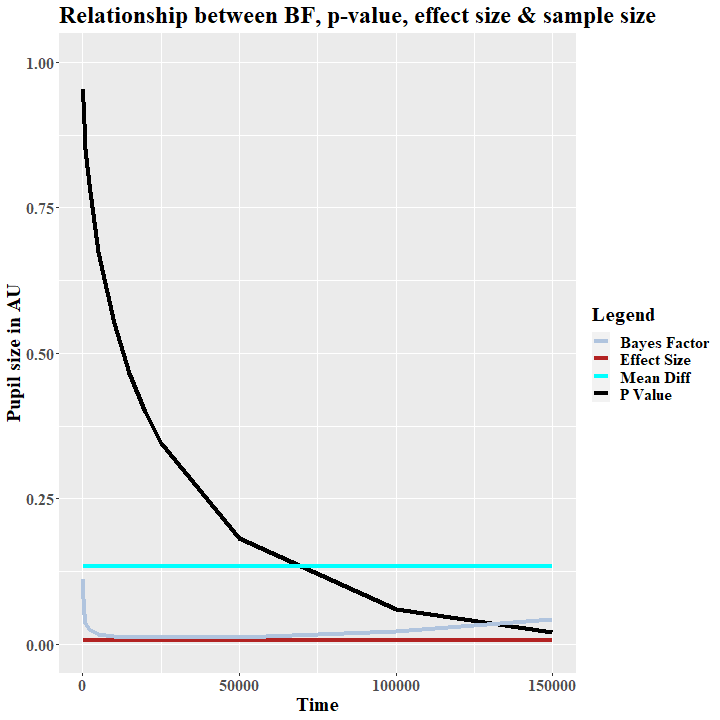
In Abbildung 3 haben wir den Einfluss der Stichprobengröße auf die Effektstärke abgebildet. Man kann erkennen, dass es schlicht und einfach keinen gibt. Die Effektstärke bleibt konstant über alle Samples.

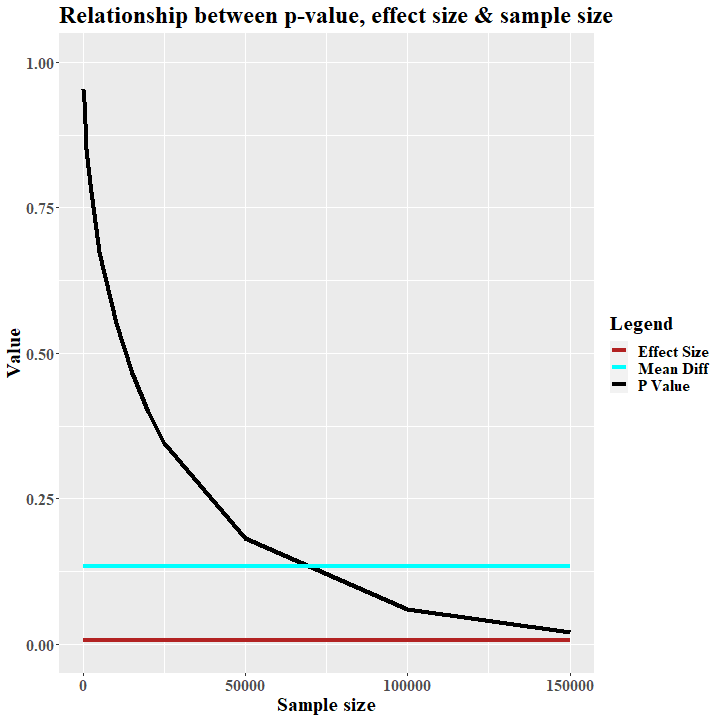
Mit Cohens (1992) Formel lässt sich die Effektstärke wie folgt berechnen:

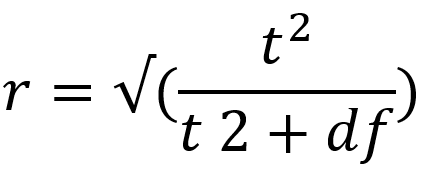
Bereits hier wird ersichtlich, dass über die Freiheitsgrade die Stichprobengröße einfach wieder herausgerechnet wird. Somit bleibt die Effektstärke unbeeinflusst. In unserem Beispiel haben wir erwartungsgemäß keinen Effekt, der über die Sample Sizes konstant bleibt (r=.005; Cohen, 1992). Bei unserer sehr großen Stichprobe von N=110000 würden wir dann die sehr widersprüchliche Aussage erhalten, einen signifikanten nicht-Effekt gefunden zu haben.

Der Vorteil der Effektstärke ist also deutlich. Gerade bei großen Stichproben ist es oft kaum möglich nicht-signifikante Ergebnisse zu erhalten. Das freut die Autoren sehr, wird aber spätestens dann unangenehm, wenn Ergebnisse nicht repliziert werden können.

Eine weitere Möglichkeiten für Hypothesentests bzw. die Auswahl oder Entscheidung zugunsten Alternativ- oder Nullhypothese bietet die Bayessche Statistik.

Bayessche Statistik und Bayes Faktor

Der Bayes Faktor bietet die Möglichkeit Hypothesen gegeneinander zu testen bzw. ist ein Instrument zur Favorisierung. Vereinfacht gesagt spiegelt er eine Tendenz wider, ob nun Null- oder Alternativhypothesen die empirischen Daten besser erklären können. Der große Vorteil der Bayesschen Statistik liegt in der Berücksichtigung von Vorinformation (a priori, Prior).

Ein sehr anschauliches Beispiel liefert Tschirk (2014) hinsichtlich der Zuverlässigkeit klinischer Tests.

Nehmen wir einmal an, ein HIV-Test hat eine 99% Sensitivität (+ als + erkennen) und eine 99% Spezifität (- als -) erkennen. Wie hoch ist also die Wahrscheinlichkeit, dass eine Person aus Österreich tatsächlich das HI-Virus hat, wenn der HIV-Test positiv wird? Als weitere Informationen steht uns die Punktprävalenz von 0.001zur Verfügung (15000 von 8.4Mio haben HIV; Stand 2014). Auch hier hilft uns wieder die Vierfeldertafel:

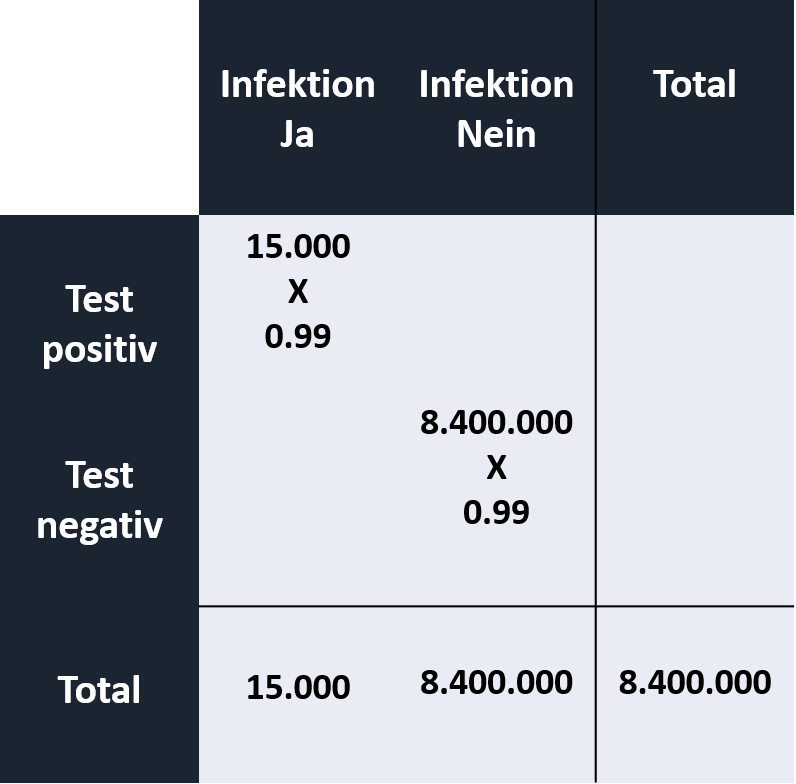
Die Anzahl der richtig positiv und richtig negativen Fälle muss mit der Spezifität und Sensitivität von jeweils 99% verrechnet werden. Die Differenzen ergeben die falsch positiven (α-Fehler) und falsch negativen (β -Fehler) Fälle:

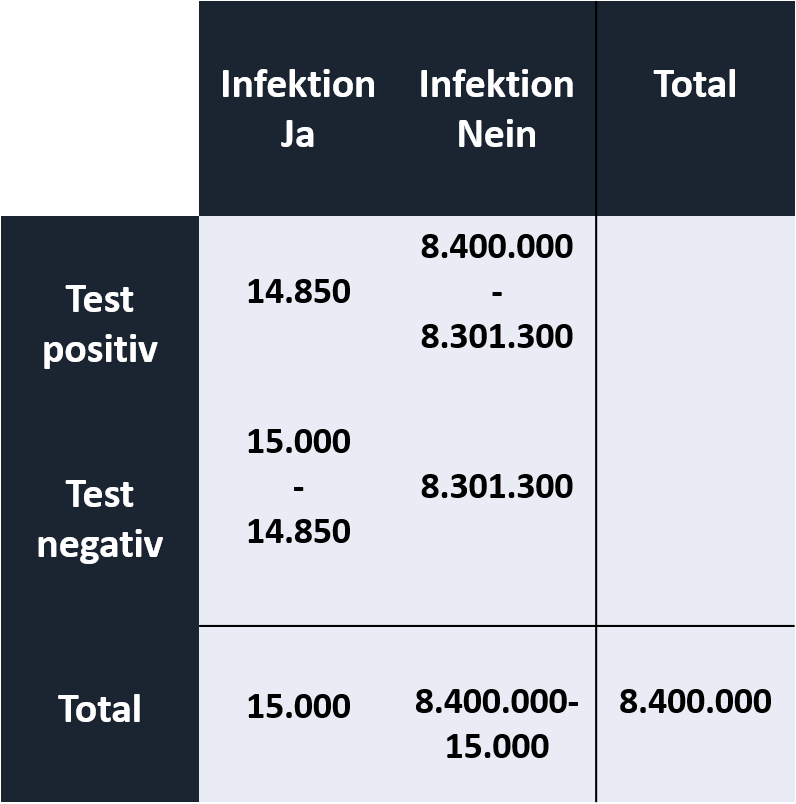
Daraus ergeben sich die genauen Fallzahlen richtig/ falsch positiv/negativ zugeordneter Personen:

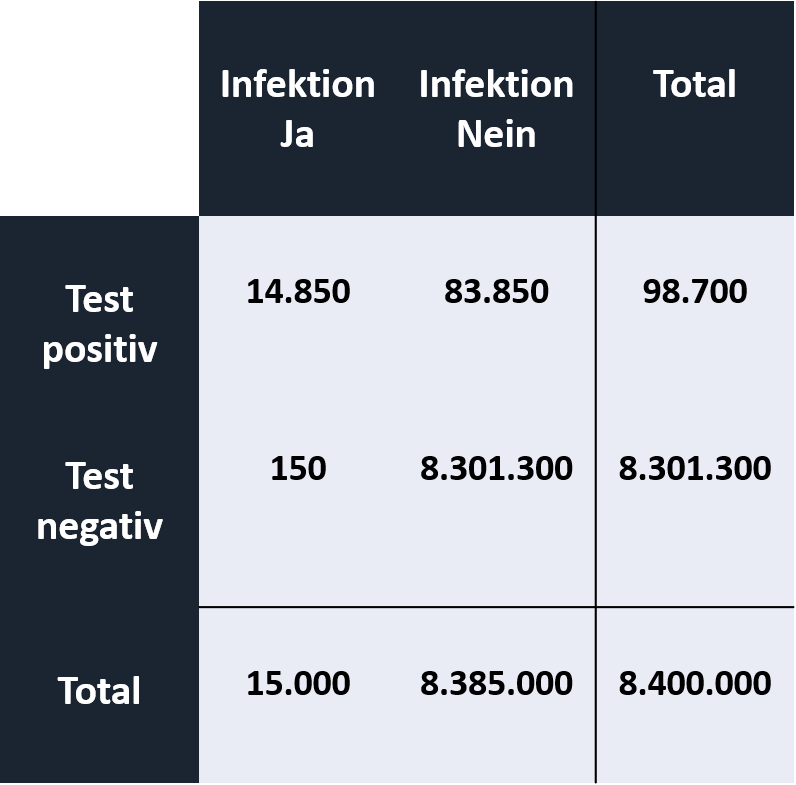
Und diese setzen wir nach dem Satz von Bayes ins Verhältnis. Also die Wahrscheinlichkeit HIV zu haben, wenn der Test positiv wurde (p(H│P)). Diese ergibt sich aus der Wahrscheinlichkeit ein positives Ergebnis zu erhalten, wenn man HIV hat, multipliziert mit der Wahrscheinlichkeit überhaupt HIV zu haben, geteilt durch die Wahrscheinlichkeit überhaupt ein positives Testergebnis zu erhalten.

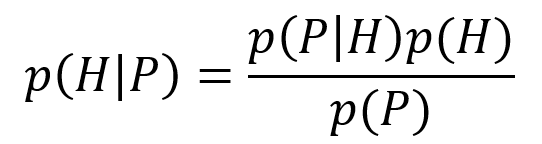
Wir erhalten das Verhältnis der richtig positiv zugeordneten Erkrankten zu der Gesamtzahl der richtig und falsch positiven Tests:

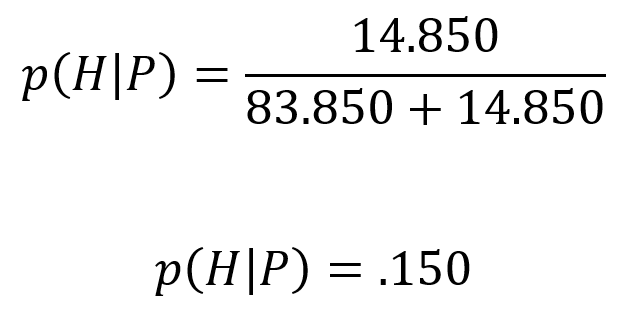
Und wenn dieses Ergebnis überraschend ist, dann ist das nicht verwunderlich, denn es ist alles andere als intuitiv. Die 99% Zuverlässigkeit führt hier zu Verwirrung. In der Psychologie spricht man von einer Ankerheuristik. Das heißt, dass diese hohe Zahl eine hohe Akkuratheit suggeriert, bevor wir eigentlich weitere Informationen haben. Denn die Wahrscheinlichkeit in Österreich zum Gegenwärtigen Zeitpunkt HIV zu haben liegt bei gerade einmal 0.178%. Und diese Vorinformation wird in der Bayesschen Statistik mit einbezogen, was sie um einiges Praxistauglicher und realitätsnäher macht.

Die Wahrscheinlichkeit als Österreicher mit dem HI-Virus infiziert zu sein, wenn man ein positives Testergebnis erhält und außer der Prävalenz, Sensitivität und Spezifität keine weiteren Daten verfügbar sind, liegt bei 15%!

Dieses Prinzip eignet sich sehr gut für das Testen empirischer Hypothesen. Bereits 1935 von Harold Jeffreys entwickelt, wird der Bayes Faktor dabei zunehmend beliebter. Er ergibt sich aus dem Verhältnis der Wahrscheinlichkeit für die beobachteten Daten unter der Annahme Alternativhypothese und der Wahrscheinlichkeit für die beobachteten Daten unter der Annahme Nullhypothese.

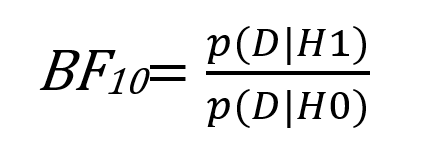
Ein großer Vorteil des BF10 liegt in seiner Robustheit bei kleinen Stichproben. Hier kann er überzeugendere Aussagen liefern. In unserem Beispiel sinkt der BF10 anfangs rasch und bleibt dann relativ konstant auf einem sehr niedrigen Wert, der einer Favorisierung der Nullhypothese entspricht (s. Abb. 3). Jedoch haben wir in diesem stark vereinfachten Beispiel keine Aussagen über a priori Annahmen definiert. Zudem haben wir die Plausibilität & Informativität der Daten und Hypothesen ignoriert. Beides spielt in der Bayessche Statistik eine wichtige Rolle. Wenn man genau hinsieht, erkennt man, dass der BF10 auch bei sehr großen Zufallsstichproben leicht steigt. Dies kann einfach dadurch erklärt werden, dass die a priori Informationen immer weniger und unsere empirischen Daten immer mehr gewichtet werden.

Hanseatic-Statistics (Krahl, 2021)

Abschließend stellen wir euch noch den Code für unsere kleine Studie zur Verfügung