Effektstärken Rechner
Test-Navigation
T-Test (unabhängig)
Für die Berechnung der Effektstärke bei einem T-Test für unabhängige Stichproben gibt es mehrere Möglichkeiten, wie zum Beispiel Cohens-d oder r (nach Cohen 1992). Besonders r ist dabei sehr nützlich, da es wie der Korrelationskoeffizient interpretiert werden kann. Es berechnet sich ganz einfach aus:
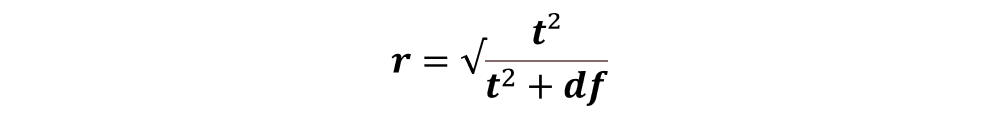
Die Interpretation ist dieselbe wie bei Korrelationen.
- r < .1 ➞ kein Effekt
- r < .3 ➞ schwacher Effekt
- r < .5 ➞ mittlerer Effekt
- r >= .5 ➞ starker Effekt
Bei Cohens-d spielt hingegen die Stichprobengröße eine Rolle zur Berechnung und eignet sich, wenn sich die Stichprobengrößen besonders stark unterscheiden. Bei gleichgroßen Stichproben ist die Formel:

Bei ungleichgroßen Stichproben ist die Formel um die gepoolte Standardabweichung erweitert:

Die Interpretation ist:
d < .2 ➞ sehr schwacher Effekt
d < .5 ➞ schwacher Effekt
d < .8 ➞ mittlerer Effekt
d < 1.2 ➞ starker Effekt
d >= 1.2 ➞ sehr starker Effekt
Mann-Whitney-U-Test
Bei nicht parametrischen Testverfahren bietet sich wieder die Effektstärke r nach Cohen (1992) an. Die Formel ist recht einfach:
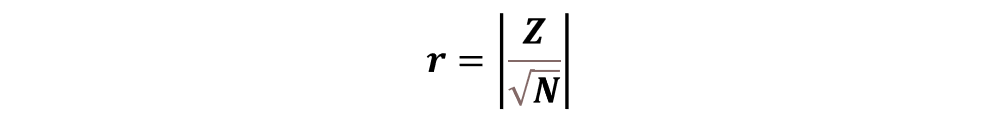
Der Betrag von Z wird durch die Wurzel der Stichprobengröße geteilt. Die Interpretation ist dieselbe wie bei Korrelationen.
r < .3 ➞ schwacher Effekt
r < .5 ➞ mittlerer Effekt
r >= .5 ➞ starker Effekt
T-Test (verbunden)
Nach Cohen (1988) lässt sich die Effektstärke für verbundene T-Tests einfach berechnen durch:
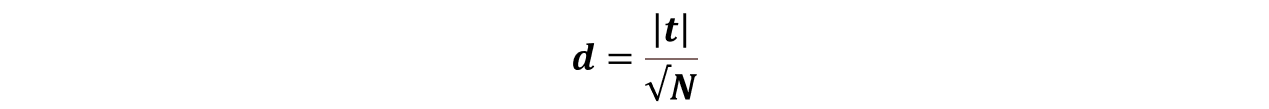
Da es ja eine verbundene Stichprobe ist, gibt es nur eine Größe von N.
Die Interpretation ist:
d < .2 ➞ sehr schwacher Effekt
d < .5 ➞ schwacher Effekt
d < .8 ➞ mittlerer Effekt
d < 1.2 ➞ starker Effekt
d >= 1.2 ➞ sehr starker Effekt
Auch hier lässt sich noch r nach Cohen berechnen.
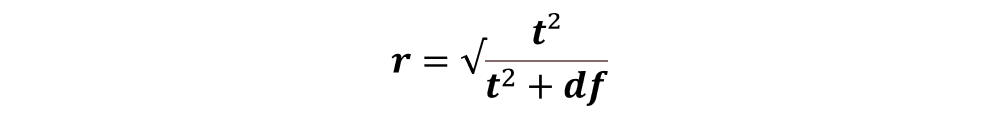
Die Interpretation ist dieselbe wie bei Korrelationen.
r < .3 ➞ schwacher Effekt
r < .5 ➞ mittlerer Effekt
r >= .5 ➞ starker Effekt
Wilcoxon-Test
Bei nicht parametrischen Testverfahren bietet sich wieder die Effektstärke r nach Cohen (1992) an. Die Formel ist recht einfach:
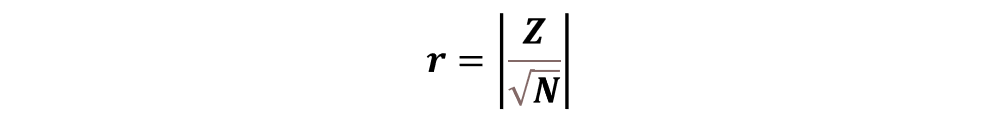
Der Betrag von Z wird durch die Wurzel der Stichprobengröße geteilt.
Die Interpretation ist dieselbe wie bei Korrelationen.
r < .3 ➞ schwacher Effekt
r < .5 ➞ mittlerer Effekt
r >= .5 ➞ starker Effekt
T-Test (einstichproben)
Nach Cohen (1988) lässt sich die Effektstärke für einstichproben T-Tests einfach berechnen durch:
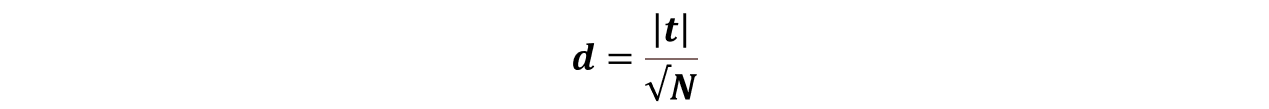
Da es eine verbundene Stichprobe ist, gibt es nur eine Größe von N.
Die Interpretation ist:
d<.2 ➞ sehr schwacher Effekt
d<.5 ➞ schwacher Effekt
d<.8 ➞ mittlerer Effekt
d<1.2 ➞ starker Effekt
d>=1.2 ➞ sehr starker Effekt
Auch hier lässt sich noch r nach Cohen berechnen.
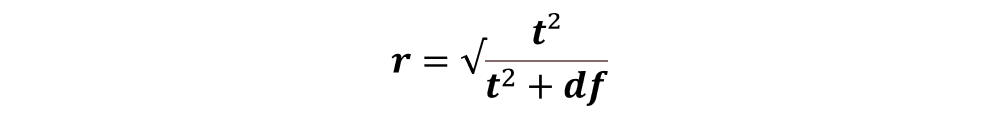
Die Interpretation ist dieselbe wie bei Korrelationen.
r < .3 ➞ schwacher Effekt
r < .5 ➞ mittlerer Effekt
r >= .5 ➞ starker Effekt
ANOVA (Gruppenvergleich, Messwiederholung, beides)
Bei Varianzanalysen (egal ob Quer-, Längs- oder gemischt-) lässt sich f nach Cohen (1992) ganz einfach aus dem partiellen ETA² berechnet. Dieses stellt, ähnlich wie bei Regressionen, ein Maß für die Varianzaufklärung dar.

Es wird die aufgeklärte ins Verhältnis zur unaufgeklärten Varianz gesetzt. Die Formel ist im Grunde dieselbe wie bei Regressionen, weil Varianzanalysen im Grunde dasselbe wie Regressionen sind. Beides sind lineare Modelle.
Die Interpretation ist:
f < .25 ➞ mittlerer Effekt
f < .40 ➞ starker Effekt
f >= .40 ➞ sehr starker Effekt
Kruskal-Wallis-Test
Bei nicht parametrischen Testverfahren bietet sich wieder die Effektstärke r nach Cohen (1992) an. Die Formel ist recht einfach:
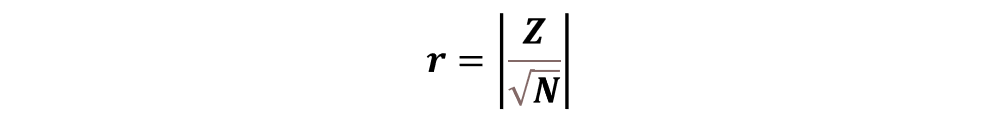
Der Betrag von Z wird durch die Wurzel der Stichprobengröße geteilt.
Die Interpretation ist dieselbe wie bei Korrelationen.
r < .3 ➞ schwacher Effekt
r < .5 ➞ mittlerer Effekt
r >= .5 ➞ starker Effekt
Friedman-Test
Bei nicht parametrischen Testverfahren bietet sich wieder die Effektstärke r nach Cohen (1992) an. Die Formel ist recht einfach:
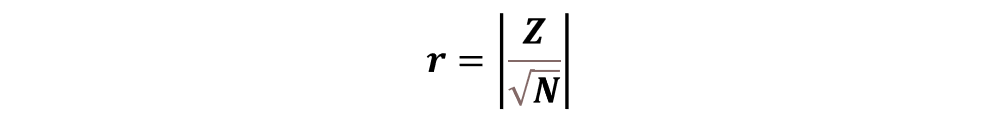
Der Betrag von Z wird durch die Wurzel der Stichprobengröße geteilt.
Die Interpretation ist dieselbe wie bei Korrelationen.
r < .3 ➞ schwacher Effekt
r < .5 ➞ mittlerer Effekt
r >= .5 ➞ starker Effekt
Chi²
Bei Chi²-Tests ist die Effektstärkenberechnung in erster Linie von der Größe der Kreuztabelle abhängig. Für einfache 2x2 Tabellen nutzt man Phi, bei größeren Tabellen Cramers-V (Cohen, 1988).


Die meisten Analyseprogramme geben Phi und Cramers-V jedoch automatisch mit aus, wie z.B. SPSS oder Jamovi.
Die Interpretation ist dieselbe wie bei Korrelationen.
φ / V < .3 ➞ schwacher Effekt
φ / V < .5 ➞ mittlerer Effekt
φ / V <= .5 ➞ starker Effekt
Korrelationen (Person, Spearman,Kendall)
Bei Korrelationskoeffizienten handelt es sich bereits um Maße für Effektstärken.
Die Interpretation ist dieselbe wie bei Korrelationen.
r < .3 ➞ schwacher Effekt
r < .5 ➞ mittlerer Effekt
r >= .5 ➞ starker Effekt
Lineare Regressionen
Hier lässt sich das f² nach Cohen (1992) ganz einfach aus dem angepassten R² berechnen. Dieses stellt, ähnlich wie bei Regressionen, ein Maß für die Varianzaufklärung dar.
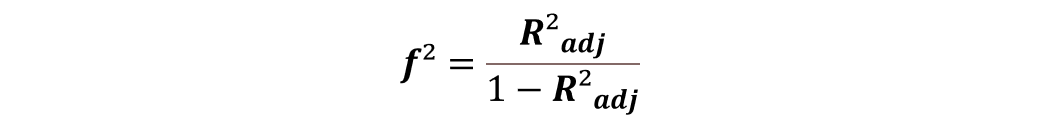
Es wird die aufgeklärte ins Verhältnis zur unaufgeklärten Varianz gesetzt. Die Formel ist im Grunde dieselbe wie bei Regressionen, weil Varianzanalysen im Grunde dasselbe wie Regressionen sind. Beides sind lineare Modelle.
Die Interpretation ist:
f² < .15 ➞ schwacher Effekt
f² < .35 ➞ mittlerer Effekt
f² >= .35 ➞ starker Effekt
Logistische Regressionen
Genau wie bei der linearen Regression wird hier das f² nach Cohen (1992) berechnet. Dafür wird das Nagelkerke R² genutzt.

Die Interpretation ist:
f² < .15 ➞ schwacher Effekt
f² < .35 ➞ mittlerer Effekt
f² >= .35 ➞ starker Effekt
Warner, R.M. (2013). Applied Statistics (2nd. Edition). Thousand Oaks, CA: SAGE.
Agresti, A. & Franklin, C. (2014). Statistics. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
Field, A. (2013). Discovering Statistics with IBM SPSS Statistics. Newbury Park, CA: Sage.
Howell, D.C. (2002). Statistical Methods for Psychology (5th ed.). Pacific Grove CA: Duxbury.
Siegel, S. & Castellan, N.J. (1989). Nonparametric Statistics for the Behavioral Sciences (2nd ed.). Singapore: McGraw-Hill.
Cohen, J (1988). Statistical Power Analysis for the Social Sciences (2nd. Edition). Hillsdale, New Jersey, Lawrence Erlbaum Associates.


